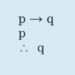If something is constructed, it is not discovered. Constructivists about a given domain of knowledge deny the following claims: (i) there is an objective, mind-independent set of facts in the given domain, (ii) there is an objective, mind-independent set of facts about justifying any conclusion about the domain, and (iii) we can explain beliefs about the domain by talking about (i) and (ii).
In a tweet, which stirred up a storm, the Mathematical Association of America wrote that math is “created by human beings.” They either said something uncontroversially true, or they have embraced a form of constructivism. If uncontroversially true, the statement says nothing more than that human beings are responsible for the advances in the domain of mathematics. As such, it does not deny (i), (ii), or (iii).
However, it is possible that the MAA intend us to understand them to be saying that the domain of study of mathematics is not of objective mathematical facts with an accompanying methodology. We don’t explain beliefs about math by saying what justifies them. Rather, they suggest that human social biases explain mathematical beliefs.

One reason to hold to such a view is that mathematics involves describing the world according to a set of interests. Perhaps the MAA are concerned that other descriptions of the world are being held at bay by a powerful, dominant group. However, thinking so doesn’t involve denying (i)-(iii). We could use many ways of describing the world without necessarily compromising our views on its objective, mind-independence. As long as one holds that views are true or false in virtue of an objective set of facts about the world and how we justify beliefs about it, there is no difficulty in using more than one set of descriptions. Indeed, mathematicians have been doing this all along.
It is, however, a further step to suggest that mathematics itself is dependent upon the descriptions human beings make of the domain. Such a view is far more radical. Due to the phrasing of the tweet, it may be that the MAA are embracing such a view. Why else would they call for people to change their minds (“it is time…to acknowledge…”). Perhaps they don’t mean us to understand them this way. I can’t say.
Nonetheless, the radical view is false. Here are two reasons:
First, consider the now much debated (on twitter) mathematical fact, 2+2=4. If 2+2=4 is constructed, then it was not true prior to its construction by human beings. Yet 2+2=4 was true before any human began to count. Thus, it is not constructed by human beings. Further, if human beings go out of existence, the fact that 2+2=4 won’t be altered in any way. It will be as true as it was before we got here.
Second, if constructivism is true, then one group of human beings constructed the fact that 2+2=4. It is possible, then, that another group of human beings construct the fact that it is false that 2+2=4. If so, then it is possibly true that 2+2=4 and that it is false that 2+2=4. But that is a contradiction. Hence, constructivism is false.
The only way to avoid arguments like these is to hold to a form of relativism. Accordingly, a constructivist will say that 2+2=4 is true only relative to a given theory. More precisely, they will say that 2+2=4 is accepted by a group according to the theory accepted by that group.
However, at least in its global form, relativism is an incoherent position to take. Consider the claim that there are no objective mind-independent facts. The claim itself is either an objective mind-independent fact or it isn’t. If it is, then global relativism is false. If it isn’t, then we have no reason to believe it.
The relativist may complain that we do have good reason to believe it. We have a pragmatic reason. After all, hasn’t the constructivist been saying that we hold beliefs due to our biases?
Let’s concede the point. We can justify our relativism pragmatically and since there is no other way of justifying any claim, we can avoid self-defeat. However, as Paul Boghossian points out, there is a further problem. Consider again our math fact, 2+2=4. Our claim that 2+2=4 amounts to an assertion-in-a-theory. Since all facts are assertions-in-a-theory, the theory itself turns out to be an assertion-in-a-theory. But so is that assertion! There could be no end to the chain. Boghossion argues that such an infinite regress has the consequence that every assertion we make is a disguised infinity of assertions that could never be expressed. But that is an absurd consequence. Thus, relativism is false.
In sum, if constructivism is true, then relativism is. Relativism is false. Hence, so is constructivism.
In this post, I have roughly followed the outline of the first two chapters of Paul Boghossian’s Fear of Knowledge (OUP, 2006).